Creating a QECC Class
To facilitate the evaluation of QECC protocols not included in PECOS, this appendix shows how to represent a QECC with a Python so can be used with PECOS. In particular, we look at representing the repetition code.
To begin, we create an empty Python file called zrepetition.py and import some useful classes:
"""
A representation of the Z-check repetition code.
"""
from pecos.circuits import QuantumCircuit
from pecos.qeccs import QECC, LogicalGate, LogicalInstruction
Subclasses of QECC, LogicalGate, and LogicalInstruction inherit numerous methods and attributes that
simplify the creation of new qeccs. If some of the inherited methods and attributes are not appropriate for a QECC,
one can typically override them.
The QECC class
We now create a class ZReptition to represent our qecc:
class ZRepetition(QECC):
def __init__(self, **qecc_params):
# Pass qecc_params to the parent class:
super().__init__(**qecc_params)
# Set variables that describe the QECC:
self._set_qecc_description()
# Create a lattice for placing qubits:
self.layout = self._generate_layout()
# Identify the sides of the QECC:
self._determine_sides()
# Identify symbols with gate/instruction classes:
self._set_symbols()
Here, the dict called qecc_params will be used to specify parameters that identify a member of the QECC’s
family. We will discuss later the method calls see in the __init__ method.
Next, we write the _set_qecc_description, which sets class attributes that describe the QECC:
def _set_qecc_description(self):
self.name = 'Z Repetition Code'
# Size of the repetition code:
self.length = self.qecc_params['length']
self.distance = 1
self.num_data_qudits = self.length
self.num_logical_qudits = 1
self.num_ancillas = self.num_data_qudits - 1
The name attribute identifies the code. The length attribute we will use to define how long the QECC is. We use
distance to determine the size of the QECC. We will be describing a repetition that only has \(Z\) checks;
therefore, the code will not detect any \(Z\) errors. For this reason, the distance is one no matter the length of
the QECC. num_data_qudits is the number of data qubits. The attribute num_logical_qudits is the number of
logical qubits we will encode with this QECC. The total number of ancillas used in all the qecc’s procedures is
equal to num_ancillas. The total number of qubits is equal to the num_qudits attribute. This attribute is
determined by the parent class QECC.
Next, we construct _set_symbols, which contain dictionaries that associate symbols to LogicalInstructions and
LogicalGates. We will describe these classes later.
def _set_symbols(self):
# instruction symbol => instr. class:
self.sym2instruction_class = {
'instr_syn_extract': InstrSynExtraction,
'instr_init_zero': InstrInitZero, }
# gate symbol => gate class:
self.sym2gate_class = {
'I': GateIdentity,
'init |0>': GateInitZero, }
Now we write the method _generate_layout, which generates the physical layout of qubits. As we will see later, a
physical layout is useful for defining the quantum circuits of the QECC protocol.
def _generate_layout(self):
self.lattice_width = self.num_qudits
data_ids = self._data_id_iter()
ancilla_ids = self._ancilla_id_iter()
y = 1
for x in range(self.lattice_width):
if x%2 == 0: # Even (ancilla qubit)
self._add_node(x, y, data_ids)
else: # Odd (data qubit)
self._add_node(x, y, ancilla_ids)
# `add_nodes` updates an attribute called `layout.`
return self.layout
Finally for the qecc, we will add the method _determine_sides to create a dictionary that defines the physical
boundary of the QECC. This information can be used by decoders to understand the geometry of the code.
def _determine_sides(self):
self.sides = {
'length': set(self.data_qudit_set)
}
Logical Instruction Classes
Now that we have created a class to represent the QECC, we will now create classes to represent logical instructions.
First create an logical instruction class, called InstrSynExtraction, that represents one round of syndrome
extraction. Similar to the ZRepitition class, we will subclass our class off of the LogicalInstruction, which is
provided by PECOS. After we do this, we will write an initialization method that receives as arguments the qecc
instance the instruction belongs to, the associated symbol, and a dictionary of logical gate parameters called
gate_params. This dictionary will come from the LogicalGate that contains the LogicalInstruction and may
alter the LogicalGate and the QuantumCircuit contained in the LogicalInstruction.
class InstrSynExtraction(LogicalInstruction):
def __init__(self, qecc, symbol, **gate_params):
super().__init__(qecc, symbol, **gate_params)
# The following are convienent for plotting:
self.ancilla_x_check = set()
self.ancilla_z_check = qecc.ancilla_qudit_set
self._create_checks()
self.set_logical_ops()
self._compile_circuit(self.abstract_circuit) # Call at end
We now include the _create_checks method, which we will use to define the checks of the QECC:
def _create_checks(self):
self.abstract_circuit = QuantumCircuit(**self.gate_params)
for qid in self.qecc.ancilla_qudit_set:
x, y = qecc.layout[qid]
# Get the data qubits to each side.
d1 = qecc.position2qudit[(x-1, y)]
d2 = qecc.position2qudit[(x+1, y)]
self.abstract_circuit.append('Z check', {qid, d1, d2}, datas=[d1, d2], ancillas=[qid])
Here we use the physical layout of the QECC to construct checks. A QuantumCircuit called abstract_circuit is
used to register each \(Z\)-type check, the qubits it acts on, and whether the qubits are used as data or ancilla
qubits. Note, check circuits such as the ones seen in Fig~ref{fig:surf-checks} are used to implement the checks. The
order of the data qubits in the datas keyword indicates the order which the data qubits are acted on by the check
circuits. The checks registered by abstract_circuit are later compiled into quantum circuits.
Now we will write the method set_logical_ops, which define the logical operators of the QECCs.
def set_logical_ops(self):
data_qubits = set(self.qecc.data_qudit_set)
logical_ops = [
{'X': QuantumCircuit([{'X': {0}}]),
'Z': QuantumCircuit([{'Z': data_qubits}])}
]
self.initial_logical_ops = logical_ops
self.final_logical_ops = logical_ops
# The final logical sign and stabilizer
self.logical_stabilizers = None
self.logical_signs = None
Here, the variables initial_logical_ops and final_logical_ops that represent the initial and final logical
operators, respectively, are set. Each of these variables are a list where each element represents a collection of
logical operators of an encoded qudit. In particular, each element is a dictionary where the keys are symbols
identified with the logical operator and the values are QuantumCircuits representing the unitaries of logical
operators.
If a logical operator encodes a stabilizer state then logical_stabilizers is a list of the strings representing the
logical operators that stabilizer the state. If the logical operator does not specifically encode a stabilizer state,
then logical_stabilizers is set to None. The variable logical_signs is a list of signs the corresponding
logical operators in logical_stabilizers. If the phase of the operators is \(+1\), then the element of
logical_signs is 0. If the phase of the operators is \(-\), then the element of logical_signs is 1. If
logical_stabilizers is None, then logical_signs is None.
We now define the initialization of the logical zero-stat:
class InstrInitZero(LogicalInstruction):
def __init__(self, qecc, symbol, **gate_params):
super().__init__(qecc, symbol, **gate_params)
# The following are convienent for plotting:
self.ancilla_x_check = set()
self.ancilla_z_check = qecc.ancilla_qudit_set
self._create_checks()
self.set_logical_ops()
# Must be called at the end of initiation.
self._compile_circuit(self.abstract_circuit)
Here, the method _create_checks is used to create check by first making a shallow copy of the abstract_circuit
of the InstrSynExtraction class. After doing this we add \(|0\rangle\) initialization of the data qubits on the
0th tick.
The _create_checks method is as follows:
def _create_checks(self):
# Get an instance of the syndrome extraction instruction
syn_ext = qecc.instruction('instr_syn_extract', **self.gate_params)
# Make a shallow copy of the abstract circuits.
self.abstract_circuit = syn_ext.abstract_circuit.copy()
# Add it the initialization of the data qubits
data_qudits = set(qecc.data_qudit_set)
self.abstract_circuit.append('init |0>', locations=data_qudits, tick=0)
The set_logical_ops method is similar to the of method of the same name in InstrSynExtraction. The difference
for this class is that a logical zero-state is encoded by the logical operator. Because of this, logical_stabilizers
is set to ['Z'] and logical_signs is set to [0].
def set_logical_ops(self):
data_qubits = set(self.qecc.data_qudit_set)
self.initial_logical_ops = [
{'X': QuantumCircuit([{'X': {0}}]),
'Z': QuantumCircuit([{'Z': {0}}])} ]
self.final_logical_ops = [
{'X': QuantumCircuit([{'X': {0}}]),
'Z': QuantumCircuit([{'Z': data_qubits}])} ]
self.logical_stabilizers = ['Z']
self.logical_signs = [0]
Logical Gate Classes
We now construct the LogicalClass classes. The construction of these classes is relatively simple compared to the
create of LogicalInstruction classes.
To begin, we write the class representing the logical identity called GateIdentity:
class GateIdentity(LogicalGate):
def __init__(self, qecc, symbol, **gate_params):
super().__init__(qecc, symbol, **gate_params)
self.expected_params(gate_params, {'num_syn_extract', 'error_free', 'random_outcome'})
self.num_syn_extract = gate_params.get('num_syn_extract', qecc.length)
self.instr_symbols = ['instr_syn_extract'] * self.num_syn_extract
Here, the initialization method includes the argument qecc and the argument symbol. These are the qecc
instance of the LogicalGate class and the string used to represent the LogicalGate, respectively. The
initialization method also accepts a keyword arguments, which are stored in the dictionary gate_params and may be
used to alter the LogicalGate and associated LogicalInstructions.
The method expected_params determines the keyword arguments that are accepted from gate_params. The number of
syndrome extraction rounds equal to 'num_syn_extract'. in the gate_params dictionary. Finally, a list of
LogicalInstruction symbols is stored in the variable instr_symbols. The instr_symbols indicates the order of
LogicalInstructions that the gate represents. The correspondence between the LogicalInstruction classes and
symbols was established by the sym2instruction_class method of the ZRepetition class.
We will also create a LogicalGate class the represents the initialization of logical zero:
class GateInitZero(LogicalGate):
def __init__(self, qecc, symbol, **gate_params):
super().__init__(qecc, symbol, **gate_params)
self.expected_params(gate_params, {'num_syn_extract', 'error_free', 'random_outcome'})
self.num_syn_extract = gate_params.get('num_syn_extract', 0)
self.instr_symbols = ['instr_init_zero']
syn_extract = ['instr_syn_extract'] * self.num_syn_extract
self.instr_symbols.extend(syn_extract)
Here, all the methods function the same way as those in the GateIdentity class.
Example Usage
Now we will look at a small example of using the ZRepetition class that we created. We begin by importing the class
from the zrepetition.py script and creating an instance of length three:
from zrepetition import ZRepetition
qecc = ZRepetition(length=3)
Now that we have created an instance, we will use the plot method that is inherited by the syndrome-extraction
instruction:
qecc.instruction('instr_syn_extract').plot()
This code results in the plot of the length three repetition code:
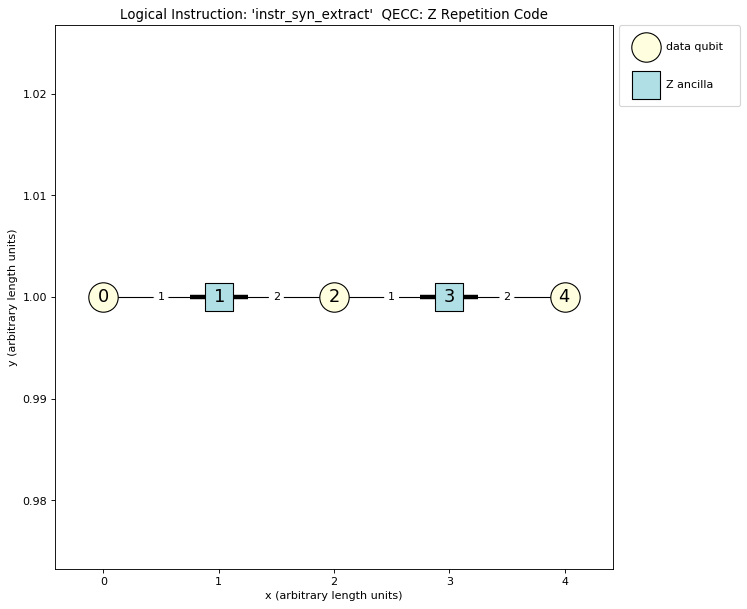
The ZRepetition class can be used just like any other qecc that comes with PECOS. For example, we can run the
following simulation:
>>> import pecos as pc
>>> depolar = pc.error_gens.DepolarGen(model_level='code_capacity')
>>> logic = pc.circuits.LogicalCircuit()
>>> logic.append(qecc.gate('ideal init |0>'))
>>> logic.append(qecc.gate('I'))
>>> circ_runner = pc.circuit_runners.Standard(seed=3)
>>> state = circ_runner.init(qecc.num_qudits)
>>> meas, err = circ_runner.run_logic(state, logic, error_gen=depolar, error_params={'p': 0.1})
>>> meas
{(1, 2): {3: {3: 1}}}
>>> err
{(1, 2): {0: {'after': QuantumCircuit([{'X': {4}}])}}}