QECCs¶
Each QECC or family of QECCs can be represented by a class. The classes available in PECOS are in the namespace qeccs. In this section we will discuss the methods, attributes, and structure of a qecc. In Creating a QECC Class, an example is given of how to construct a new QECC class, which can be used by PECOS.
The primary role of a qecc is to provide the quantum circuits of QEC protocols associated with the qecc such as the logical-state initialization, logical gates, and logical measurements. In the following, we will look at some examples of qecc classes and how they encapsulate QEC procedures.
Methods¶
The minimal methods expects for a qecc:
gate |
Returns an instance of a requested logical gate. |
instruction |
Returns an instance of a requested logical instruction. |
plot |
Plots the physical layout of qudits. |
Attributes¶
name |
Name of the QECC. |
qecc_params |
Dictionary of parameters. |
distance |
Minimum number of single qudit operations that results in a logical error. |
num_logical_qudits |
Number of logical qudits. |
num_data_qudtis |
Number of data qudits. |
num_ancilla_qudits |
Number of ancillas. |
num_qudits |
Number of qudits. |
qudit_set |
Set of qudit labels used internally in the qecc. |
data_qudit_set |
Set of data qudit labels used internally. |
ancilla_qudit_set |
Set of ancilla qudit labels used internally. |
layout |
A dict of qudit label to position tuple. |
sides |
A dict describing the geometry of the qecc. |
An Instance¶
Currently, the namespace qeccs contains classes representing the surface code on the 4.4.4.4 lattice (Surface4444) [Kit97b], the medial surface-code on the 4.4.4.4 lattice (SurfaceMedial4444) [BMD07], and the color-code on the 4.8.8 lattice (Color488) [BMD06].
An example instance of a Surface4444 that represents a distance 4 surface code is given here:
>>> import pecos as pc
>>> surface = pc.qeccs.Surface4444(distance=3)
As seen in Listing 6.20, parameters are used to identify a member of the code family.
For Surface4444, either the keyword distance or the keywords height and width are used to specify a member. If distance is used, then a representation of a square surface-code patch will be created. The SurfaceMedial4444 class will take the same keywords as code family parameters as the Surface4444 class. The Color488 class only accepts distance as a keyword.
Logical Gate¶
The class LogicalGate represent a collection of quantum circuits that act on logical qubits. Each LogicalGates is identified by a symbol (string). Using this symbol, the gate method of a qecc can be used to obtain an instance of a corresponding LogicalGate instance:
>>> surface = pc.qeccs.Surface4444(distance=3)
>>> identity = surface.gate('I')
In the above code, the symbol 'I' is used to retrieve a logical gate corresponding to identity (syndrome extraction).
Keyword arguments may be used to modify LogicalGates:
>>> surface = pc.qeccs.Surface4444(distance=3)
>>> # Get an identity gate with only one round of syndrome extraction.
>>> identity = surface.gate('I', num_syn_extract=1)
Here the keyword argument num_syn_extract is used to explicitly request an identity with only one round of syndrome extraction. Typically, the number of rounds of syndrome extraction for an identity gate is equal to the QECC’s distance.
The main use for LogicalGate instances is as logical operations in the logical analogs of quantum circuits, which are described in Logical Circuits
Logical Instruction¶
A LogicalGate is composed of a sequence of LogicalInstructions. A LogicalInstruction represents a collection of quantum circuits. Often these collections are repeated or used in multiple LogicalGates. An example of a LogicalInstruction is one round of error correction.
Like LogicalGates, LogicalInstuctions are represented by symbols (strings). The instr_symbols attribute of a LogicalGate can be use to retrieve a list of symbols corresponding to the LogicalInstuctions that form the LogicalGate:
>>> surface = pc.qeccs.Surface4444(distance=3)
>>> identity = surface.gate('I')
>>> identity.instr_symbols
['instr_syn_extract', 'instr_syn_extract', 'instr_syn_extract']
>>> # Request an identity with a single round of syndrome extraction.
>>> identity = surface.gate('I', num_syn_extract=1)
>>> identity.instr_symbols
['instr_syn_extract']
In the following, we see how to retrieve an instance of the 'instr_syn_extract' instruction and then see what QuantumCircuit it represents:
>>> surface = pc.qeccs.SurfaceMedial4444(distance=3)
>>> # Get the LogicalInstruction instance representing the syndrome-extraction instruction.
>>> instr = surface.instruction('instr_syn_extract')
>>> instr.circuit
QuantumCircuit([{'init |0>': {0, 16, 4, 5, 6, 10, 11, 12}}, {'H': {0, 16, 11, 5}}, {'CNOT': {(15, 12), (11, 14), (8, 6), (5, 7), (13, 10), (0, 2)}}, {'CNOT': {(9, 12), (2, 6), (7, 10), (11, 15), (0, 3), (5, 8)}}, {'CNOT': {(7, 4), (16, 13), (14, 10), (11, 8), (5, 1), (9, 6)}}, {'CNOT': {(3, 6), (16, 14), (11, 9), (5, 2), (8, 10), (1, 4)}}, {'H': {0, 16, 11, 5}}, {'measure Z': {0, 16, 4, 5, 6, 10, 11, 12}}])
Plotting¶
Both qeccs and LogicalInstuctions have a method called plot that will generate a plot that represents the object. These plots can be useful in understanding the structure of a QECC and its logical instructions.
The following is an example of using the plot method for a qecc:
>>> surface = pc.qeccs.SurfaceMedial4444(distance=3)
>>> surface.plot()
This results in the plot seen in:

The plot of LogicalInstructions often indicates the sequence of gate operations. An example of a plot of the syndrome extraction instruction of surface be obtained by the following lines:
>>> surface = pc.qeccs.SurfaceMedial4444(distance=3)
>>> syn_extract = surface.instruction('instr_syn_extract')
>>> syn_extract.plot()
The resulting plot is seen in:
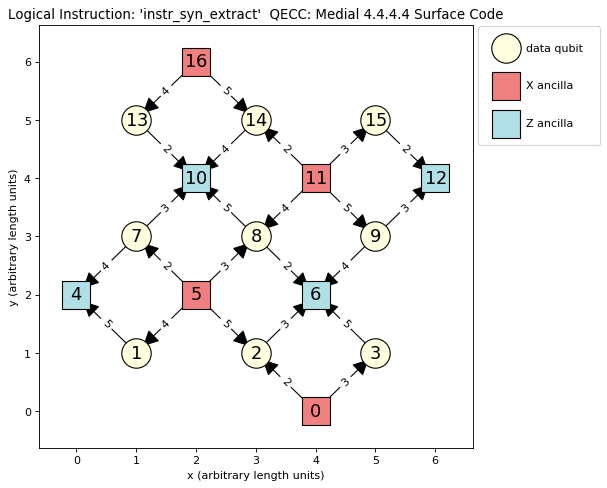
The previous figure depicts the syndrome-extraction logical-instruction of a distance-three, medial surface-code. Red squares represent the ancillas involved in X checks, the blue squares represent the ancillas involved in Z checks, and the cream circles represent the data qubits. The numbers inside the squares and circles are labels of the qubits as used in QuantumCircuits. The edges indicate the CNOTs used in the checks. The thicker end of each edge denotes the qubit that is the target of the CNOT. The numbers labeling the edges are ticks when the corresponding CNOT is applied.